Abstract

A recent econometric literature has critiqued the use of regression discontinuities where administrative borders serve as the ‘cutoff’. Identification in this context is difficult since multiple treatments can change at the cut-off and individuals can easily sort on either side of the border. This note extends the difference-in-discontinuities framework discussed in Grembi et al. (2016) to a geographic setting. This paper formalizes the identifying assumptions in this context, which will allow for the removal of time-invariant sorting and multiple treatments similar to the difference-in-differences methodology.

5-Minute Summary

An increasingly popular estimation strategy involves using administrative borders as cut-offs in a regression discontinuity (RD) setting, where the ‘running variable’ is the distance to the border. Identification using the ‘continuity assumption’ is problematic in these settings since even in the absence of treatment people can sort on either side of borders (e.g. for lower taxes or better schools) and many policies change at the same border (tax-laws, police-services, schools, etc.).

This paper extends the proposed ‘difference-in-discontinuities’ estimator (Grembi et al. (2016)) to the geographic RD setting. The intuition of the difference-in-discontinuities design is very similar to the difference-indifferences design. A pre-treatment RD identifies the time-invariant effects of other laws as well as the discontinuity in outcomes due to time-invariant sorting. A post-treatment RD identifies those previous two discontinuities plus the one caused by the treatment of interest. The difference between the two identifies the treatment effect.

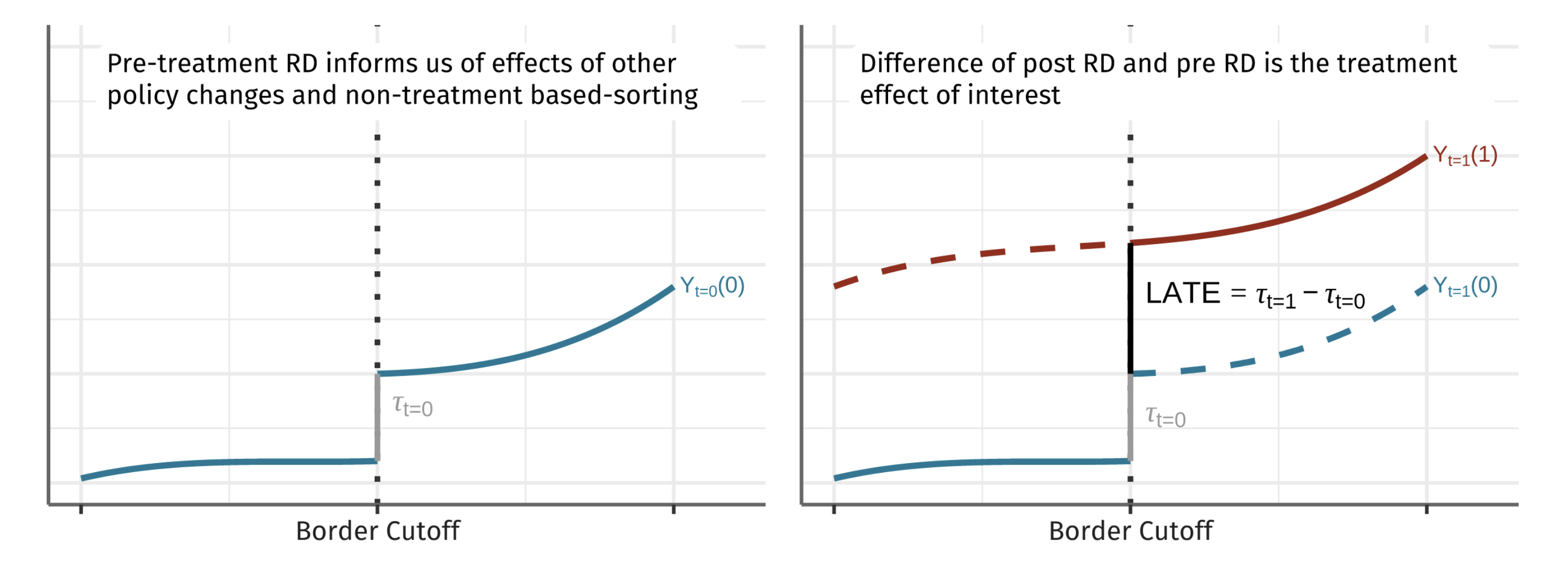
The paper goes into the theoretical assumptions that are necessary for the diff-in-disc method to work, but here is the intuition:

• The untreated potential outcome must be continuous at the cut-off. Note that this untreated potential outcome is conceptually the outcome without any treatments (including the ones implemented in the past). A time-invariant “jump” discontinuity will be differenced out.

• The effects of all other treatments must be “fully observed” in the pre-period. If not, then you can’t disentangle the effects of the treatment of interest from the other treatments.

• There can be no sorting in the post-period from the treatment of interest. This is a standard assumption in RD that allows units near the cutoff to be similar in covariates.

The paper concludes with a discussion of how to estimate the diff-in-disc estimator in a single RD regression on first-differenced outcomes using the modern robust RD tools. For more details on modern RD tools, see Cattaneo et. al. (2019)